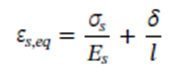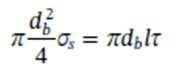Nuevo Modelo Equivalente Tensión-Deformación en Armaduras de Estructuras de Hormigón para Predecir la Fisura en Juntas y Mejorar la Durabilidad
José Ramón Díaz de Terán López
Resumen.
La durabilidad de las infraestructuras de hormigón es muy dependiente de la apertura de fisura. Las juntas de hormigonado de las estructuras de hormigón armado (RC) son elementos muy sensibles y se dan tanto en el armado “in situ” como en estructuras de hormigón prefabricado. Las normas actuales no son capaces de predecir con precisión ni del lado de la seguridad la apertura de fisura en juntas. En esta publicación se basa en una investigación previa que propone un nuevo modelo de tensión-deformación del acero para afrontar el cálculo de fisuras en juntas con precisión y mejorar el análisis de durabilidad de las juntas de hormigonado.
Palabras clave: fisuración; juntas de hormigonado; adherencia, elementos finitos, armaduras embebidas, ley tensión-deformación equivalente no lineal.
Introducción y presentación del modelo.
Las estructuras de hormigón armado (RC) constituyen una gran parte del stock de infraestructuras existentes. La mejora de su durabilidad es una cuestión crítica de cara a la sostenibilidad de las mismas. Para hacerse una idea, en el Reino Unido, la reparación y mantenimiento representan el 45% de la inversión en infraestructuras (1).
La durabilidad de las infraestructuras de hormigón está muy influenciada por la apertura de fisuras. Uno de los componentes más sensibles de las estructuras de RC son las juntas de hormigonado, que aparecen en las estructuras prefabricadas e “in situ”. Como muestra, entre el 7 y el 8% del coste de mantenimiento de puentes en Francia es debido al estado de las juntas en los mismos (2). Por otro lado, el Departamento de Transportes de Reino Unido, cifra en 755 millones de libras las reparaciones asociadas a corrosión de armaduras en ese país (3). Sin embargo, los códigos actuales no aportan una formulación lo suficientemente precisa como para predecir la apertura de fisura en juntas, si bien estudios previos aportan fórmulas empíricas, basadas en los códigos existentes, para predecir las mismas, aplicando un factor de reducción al momento de fisuración del hormigón en las mismas, logrando un nivel de precisión elevado y del lado de la seguridad (4).
Dado que las estructuras de hormigón armado están formadas por una matriz de hormigón y una armadura de acero, siempre que se quiera predecir adecuadamente su comportamiento debe considerarse la interacción entre acero y hormigón. Hay varias maneras de modelar con elementos finitos una estructura de RC, la primera es considerando un reparto uniforme de la armadura en toda la matriz, lo cual es simple de introducir en el modelo y no implica un gran esfuerzo computacional, pero se pierde precisión. La segunda manera es introduciendo separadamente elementos de tipo barra para el acero y ligarlos a los elementos que representan al hormigón mediante elementos de tipo interfaz, sin embargo, este procedimiento demanda mucho tiempo para generar el modelo y es exigente desde el punto de vista computacional. El tercer procedimiento es mediante barras “embebidas”, que aportan suficiente precisión con un coste computacional y de modelado moderados.
Los modelos con barras “embebidas” asumen adherencia perfecta entre acero y hormigón, si bien esta situación no se presenta en la realidad, por lo que los modelos así construidos, implican una mayor rigidez y menor fisuración del conjunto estructural que la que realmente se produce. De cara a modelar de una manera más precisa el conjunto formado por el acero y el hormigón, se hace necesario incluir, de algún modo, los efectos equivalentes a una imperfecta adherencia entre acero y hormigón. Esto puede realizarse mediante una modificación de la ley de tensión-deformación del acero. A este respecto, trabajos previos (5) proponen un modelo con rigidez reducida equivalente y límite elástico reducido equivalente para el acero, tal y como propusieron Belarbi y Hsu (6), ecs. 1 y 2.
En las ecs. (1) y (2) l es la longitud de transmisión de adherencia entre hormigón y acero, δ es el desplazamiento máximo entre barras de acero y hormigón, fcr es la resistencia a tensión de fisuración del hormigón, fy es el límite elástico del acero y ρ es la cuantía de acero.
Lo que se muestra a continuación es un paso más para avanzar en este modelado, mediante una ley de tensión-deformación equivalente no lineal para el acero y que incluya el modelo de adherencia proporcionado por el Código Modelo 2010 (figura 1), basado a su vez en el modelo de adherencia de Eligehausen (7), por ser uno de los más extendidos y aceptados internacionalmente. Dicho modelo se basa en varios segmentos que se corresponden con las diferentes fases que se producen durante un proceso de carga monotónico (8) (9). En un primer tramo, antes de la fisuración, la deformación de acero y del hormigón es la misma, pero después de la fisuración, las fuerzas de tracción son transferidas al acero y debido a los desplazamientos relativos entre acero y hormigón se generan las tensiones de adherencia.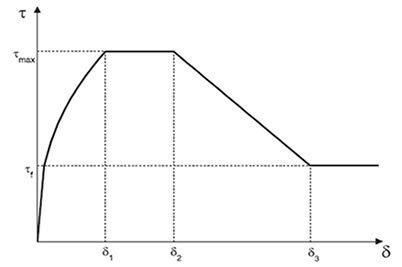
Figura 1. Modelo de adherencia del Código Modelo 2010.
La incorporación del modelo de adherencia a la ley de tensión-deformación del acero se realiza mediante la ecuación 3 y mediante la expresión clásica del equilibrio de fuerzas en “pull-out” tests, ec. 4. Para simplificar el manejo algebraico de las expresiones, se sugiere interpolar el primer tramo del modelo de adherencia del Código Modelo mediante una expresión racional.
(3) 
(4)
En dichas ecuaciones, εs,eq es la deformación equivalente del acero, δ es el deslizamiento relativo entre el hormigón y el acero, db es el diámetro de las barras de acero, σs la tensión en el acero, Es el módulo de rigidez del acero y τ la tensión tangencial por adherencia entre el acero y el hormigón.
La ley de tensión-deformación equivalente para barras embebidas se obtiene aislando el deslizamiento relativo entre barras de acero y hormigón δ en la ecuación 3, sustituyendo el valor del mismo en el modelo de adherencia e insertando las tensiones tangenciales así obtenidas en la ecuación de equilibrio 4.
Procedimiento.
La validación del modelo de tensión-deformación equivalente para el acero (Figura 2) se ha llevado a cabo mediante modelos de elementos finitos realizados con DIANA considerando adherencia perfecta (Figura 2. A), un modelo tensión-deformación del acero modificado con longitud de transmisión de adherencia inferior a la del Código Modelo 2010 (Figura 2. C) y un modelo tensión-deformación del acero modificado con la longitud de transmisión de adherencia propuesta por el Código Modelo 2010 (Figura 2. D), con los resultados de los ensayos realizados en el Laboratorio de Materiales y Estructuras de la Escuela de Ingeniería Civil de la Universidad de Castilla-La Mancha (Figura 2. HSC-C) y con la fórmula basada en la de la EHE para apertura de fisura con factor de reducción del momento crítico de fisuración en la junta(Figura 2. B) (4).
Los ensayos de losas consistieron en losas de 0.285m x 0.6m x 2.9m, con 2 fases de hormigonado, con la junta de hormigonado a 1.25m de uno de los extremos. Estas losas fueron ensayadas a flexión con 4 puntos, considerando una luz de 2.4 m y que la carga se aplicaba en 2 puntos separados 0.6m, en el centro de luz. Las juntas estaban cosidas con 6 barras de acero de 20mm de diámetro. Los ensayos se realizaron con control por desplazamiento a una tasa de 1.2 mm/min. El hormigón evaluado fue de alta resistencia, con una resistencia media a compresión de 54 MPa y las armaduras de acero B500S.
La simulación numérica consistió en modelos de elementos finitos F.E.M. en 2D con geometría y materiales similares a los ensayados en laboratorio. El programa utilizado para la simulación fue DIANA® 9.6 y los elementos fueron Quadrilateral 4 nodes (10) de dimensiones 10mm x 10mm con espesores de 600 mm. También se usaron elementos Interface L8IF para similar la junta de hormigonado. La simulación fue no lineal y con fisuración, plasticidad y elasticidad no lineal directamente derivada del modelo de tension-deformación que se ha propuesto. La convergencia de los modelos se basó en el criterio de energía con un número máximo de 500 iteraciones utilizando el método Newton Raphson. La tolerancia en la convergencia se estableció un valor de 0.01.
Comparación de resultados y discusión.
Durante la evaluación del modelo con los ensayos (Figura 2), se comprobó que el efecto de la longitud de transmisión de adherencia l es un parámetro importante y que el valor propuesto por el Código Modelo, es adecuado de cara a predecir la apertura de fisura y deflexión global de las losas. Dicho valor corresponde con la mitad de la distancia media entre fisuras, es decir, que depende de la cuantía de armadura.
Los resultados (Figura 2) muestran que hay un alto grado de coincidencia con los resultados obtenidos experimentalmente en laboratorio (Figura 2. HSC-C) y con los previstos mediante la fórmula modificada mediante factor de corrección del momento de fisuración del hormigón en la junta (Figura 2. B) (4), no sólo respecto a apertura de fisura sino respecto a deflexión de la losa. De hecho, se puede apreciar que, sin tener en cuenta la imperfección de adherencia entre armadura y hormigón, la predicción de apertura de fisura es inferior a la que realmente aparece (Figura 2. A), lo cual cae del lado de la inseguridad y no permite un buen ajuste del diseño a las condiciones de durabilidad reales, mientras que la predicción basada en el modelo tensión-deformación equivalente, que contempla la imperfección de la adherencia es mucho más precisa (Figura 2. D) o cae del lado de la seguridad si la longitud de transmisión l se infraestima (Figura 2. C) y permite predecir la apertura de fisura de manera que la durabilidad se pueda garantizar.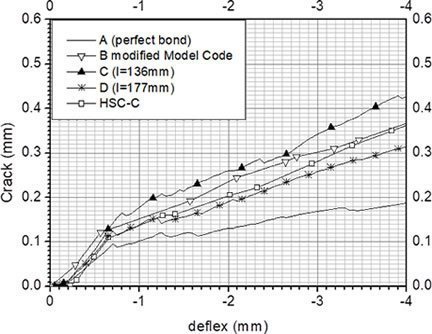
Figura 2. Apertura de fisura para varias hipótesis.
Una descripción más detallada del modelo, los resultados y las conclusiones puede ser consultada en artículos ya publicados (8) y (9).
Referencias.
(1) Van Breugel K. Is there a Market for self-healing cement based materials? Proceedings of the First International Conference of Self-Healing Materials. Noordwijk aan Zee. 2007.
(2) Lima J.M, de Brito J. Inspection survey of 150 expansion joints in road bridges. Engineering Structures 2009; 31(5): 1077-84.
(3) Ann K.Y, Ahn J.H, Ryan J.S. The importance od chloride contente at the concrete surfasse in assessing the time corrosion of steel in concrete structures. Construction and Building Materials 2009; 23(1): 239-45.
(4) Diaz de Teran J.R, Turmo J, Jorquera J.J, Barragan B, Ramos G, Aparicio A. Optimization of in situ construction of concrete decks: flexure tests of compact splices of reinforcements between phases. Construction and building materials 2013; 41: 191-203.
(5) Dehestany M, Mousavi S. Modified steel bar model incorporating bond-slip effects for embedded. Construction and Building Materials 2015; 81: 284-290.
(6) Belarbi A, Hsu T. Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. ACI Struct J 1994; 4: 91.
(7) Eligehausen R, Popov E, Bertero V. Local bond stress-slip relationships of deformed bars under generalized excitations. Rep. UCB/EERC-83/23. Berkeley: Univ of California. Earthquake Engineering Research Center; 1983.
(8) Díaz de Terán J.R, Haach V.G. Equivalent stress-strain law for embedded reinforcements considering bond-slip effects. Engineering Structures 2018; 165: 247-253.
(9) Díaz de Terán J.R, Haach V.G. Crack opening prediction at casting joints with a new modified stress-strain law for embedded reinforcement. Construction and Building Materials 2017; 157: 668-675.
(10) TNO DIANA BV. DIANA Finite Element Analysis User’s Manual release 9.6. Delft: Delftechpark 19a, 2628 XJ; 2014.
