Abstract
El fenómeno de la socavación puede poner en peligro la operatividad y la seguridad de las estructuras offshore comprometiendo su estabilidad global. Tras realizar una exhaustiva búsqueda bibliográfica para entender mejor la importancia de este fenómeno, sorprende el hecho de que la gran mayoría de las investigaciones promovidas para estudiar y entender mejor el origen y el desarrollo de este fenómeno han estado centradas en entornos fluviales, bajo condiciones de corriente continua, como es el caso de las cimentaciones que se encuentran situadas en los cursos de los ríos. Aunque también hay que destacar, que en la última década, y debido al crecimiento del mercado de la eólica marina, han empezado a surgir interesantes estudios enfocados en la caracterización de este fenómeno en el entorno marino. Hecho que resulta de especial interés, teniendo en cuenta que estas estructuras se encuentran sometidas de forma simultánea a los efectos de las corrientes, las mareas y el oleaje.
Ante esta carencia de investigaciones, y conscientes de la importancia de desarrollar nuevas soluciones para los retos existentes en el campo de la energía eólica marina, dentro del grupo de investigación “Medio Marino, Costero y Portuario y otras Áreas Sensibles” de la Universidad Politécnica de Madrid (UPM) se llevó a cabo la Tesis Doctoral “Caracterización de los sistemas de protección basados en materiales naturales destinados al control de la socavación en obras marítimas presentes en instalaciones eólicas marinas”. Dicha investigación tuvo como objetivo principal el desarrollo de nuevas recomendaciones para mejorar y optimizar el diseño de estas estructuras de protección frente a la socavación, teniendo en cuenta no sólo los parámetros geométricos de las cimentaciones de los aerogeneradores, o la propia erosión, sino también, variables características del oleaje como la altura de ola, el periodo o la longitud de onda, así como la profundidad o la batimétrica donde se encuentra instalada la cimentación.
Para llevar a cabo esta investigación, se realizó una exhaustiva revisión de la información existente sobre parques eólicos offshore dentro de la Unión Europea. Analizando desde la primera experiencia offshore en 1991 (Dinamarca), hasta las recientes propuestas de implantación en Reino Unido. Dichas estructuras se encuentran instaladas en aguas de transición con profundidades en torno a los 30 m de profundidad, y en la gran mayoría de los casos las cimentaciones fueron de tipo monopilote, de medio y gran diámetro.
En primer lugar, la investigación arrancó definiendo en cada caso de estudio las principales características de la cimentación, el clima marítimo, la correlación entre la altura de ola y el periodo asociado a una determinada recurrencia, y el tipo de protección empleado en su diseño (peso medio de las piezas, diámetro nominal en el caso de protección de escollera, espesor y comportamiento).
Teniendo en cuenta la experiencia existente de los parques eólicos offshore en funcionamiento, el análisis de los datos de diseño, las bases de datos sobre clima marítimo y la interacción suelo estructura; el parámetro de altura de ola adimensional (H0), la extensión de la erosión (Lext) y la cuantificación de la máxima profundidad de socavación fueron calibrados para un diseño preliminar de las protecciones alrededor de pilas de gran diámetro, obteniéndose valores iniciales para H0 entre 6 y 15, y valores para el diseño de la extensión de las protecciones entre L/4 y L/2 (L, longitud de onda en el pié del pilote aislado).
Introducción
El deseo de mantener el crecimiento exponencial de la energía eólica marina en Europa está inevitablemente asociado a la necesidad de mejorar el diseño de estas estructuras, y a seguir optimizando los costes presentes en sus implementaciones. La experiencia a corto plazo en este campo supone que se establezcan nuevas metodologías con el objetivo de elaborar recomendaciones para todos los pasos necesarios a tener en cuenta en el diseño de estas estructuras [1]. Por otro lado, durante estos últimos años, también ha sido importante conocer cómo la propia presencia de los parques eólicos puede afectar a los procesos litorales, para prevenir o evitar dicho impacto [2].
Un gran número de parques eólicos offshore se encuentran actualmente operativos en Europa. Las cimentaciones de tipo monopilote siguen siendo las subestructuras más habituales en la instalación de aerogeneradores marinos. De acuerdo a las últimas estadísticas [3], el 81,7% de todas las unidades instaladas desde 1991 presentan una cimentación de tipo monopilote, seguido por un 6,22% cimentadas mediante estructuras de gravedad (GBS) (ver Figura 1). Los datos recogidos en esta investigación se refieren a ambos tipos de subestructuras, aunque sólo se obtuvieron datos de dos parques eólicos cimentados sobre una subestructura de gravedad
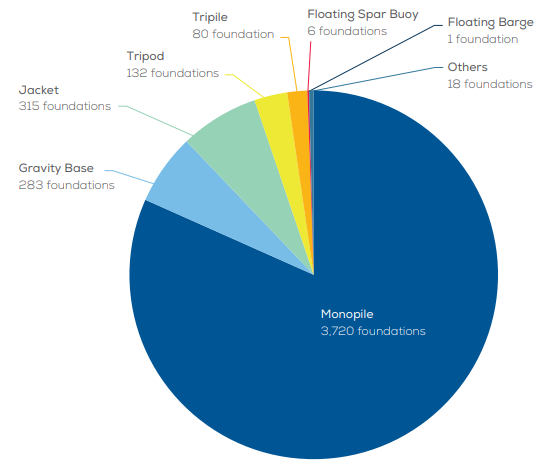Figura 1: Tipos de subestructuras presentes en los parques eólicos Europeos [3].
Los agentes del medio físico como el oleaje, la corriente o el viento juegan un papel fundamental en el diseño de estructuras offshore. Conscientes de la importancia de estas variables, esta investigación surge ante la carencia de criterios existentes en cuanto a la elección de variables climáticas para el diseño de estas estructuras. Como es evidente, la sensibilidad de este problema ante la mecánica de ondas, se encuentra fuertemente relacionado con el periodo medio del oleaje (Tm) y la longitud de onda (L).
Como consecuencia, a lo largo de la investigación se ha impuesto la necesidad de introducir monomios climáticos sancionados por la experiencia, como el parámetro de altura de ola adimensional (H0). Proponiéndose el uso de formulaciones que permitan expresar la extensión de las protecciones frente a la socavación en función del oleaje en profundidades de transición.
Para esta investigación, ha sido fundamental considerar la experiencia de algunos parques eólicos europeos en funcionamiento, el análisis de los datos de diseño, el clima marítimo y la interacción suelo estructura. Todo ello hizo posible la calibración de del parámetro de altura de ola adimensional (H0), así como el dimensionamiento de la máxima extensión y profundidad del fenómeno de la socavación.
La información empleada durante la investigación ha sido recopilada a través de diferentes estudios y artículos publicados hasta la fecha. De este modo, los parques eólicos estudiados fueron seleccionados de acuerdo a la información encontrada. La Figura 2 muestra la localización de los parques eólicos offshore europeos considerados en este estudio.
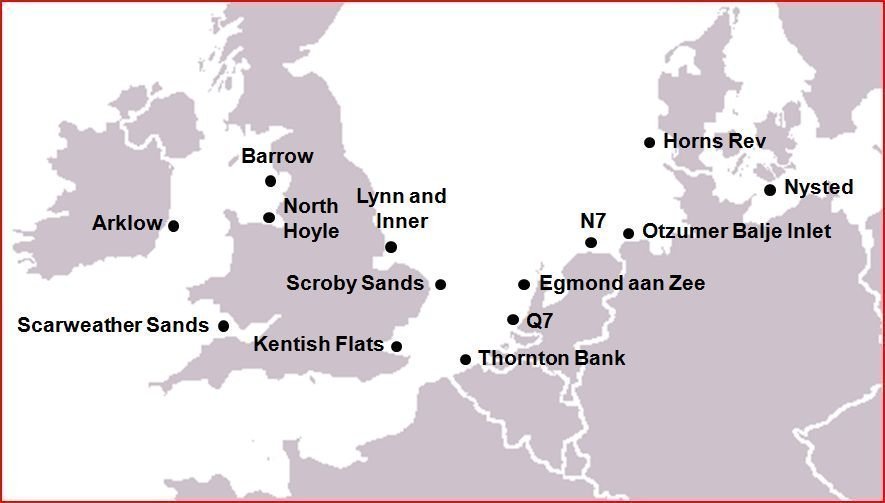Figura 2: Locación de los parques eólicos offshore estudiados.
Reino Unido sigue siendo a día de hoy el mercado más grande, agrupando más de la mitad de toda la capacidad de energía eólica offshore instalada en Europa, y teniendo además un futuro muy prometedor debido al gran apoyo de su gobierno. Alemania, Dinamarca, Holanda, Bélgica y Suecia siguen a Reino Unido en esta apuesta de fomentar el crecimiento de la energía eólica en Europa.
A continuación, en la Tabla 1 se muestra la información principal de los parques eólicos offshore (tipo de cimentación, información del clima marítimo y especificaciones técnicas de las turbinas) considerados en la investigación.
Tabla 1: Información característica de los parques eólicos offshore.
| Nombre | Año de instalación | Cimentación | Diámetro Monopila [m] | Numero de turbinas | Capacidad nominal turbinas [MW] | Prof. [m] | Altura de ola significante (Hs[m]) | Periodo pico (Tp[s]) | Velocidad pico de corriente (Um[m/s]) |
|---|---|---|---|---|---|---|---|---|---|
| N7 (Alemania) | 1997 | Monopila | 6 | 1 | – | 7 | 4,6 | 16,1 | 1,3 |
| HORNS REV (Dinamarca) | 2002 | Monopila | 4,25 | 80 | 2 | 6-14 | 5,2 | – | – |
| SCARWEATHER SANDS (UK) | 2003 | Monopila | 2,2 | 30 | 3,6 | 6 | 3,6 | 6 | 1,1 |
| OTZUMER BALJE INLET (Alemania) | 2003 | Monopila | 1,5 | 1 | – | 11,7 | – | – | 1,4 |
| NORTH HOYLE (UK) | 2003 | Monopila | 4 | 30 | 2 | 7-11 | 4,78 | 6,8 | 1,17 |
| SCROBY SANDS (UK) | 2004 | Monopila | 4,2 | 30 | 2 | 3-12 | 2,25 | – | 1,65 |
| ARKLOW BANK (Irlanda) | 2004 | Monopila | 5 | 7 | 3,6 | 2-6 | 5,6 | – | 2 |
| NYSTED (Dinamarca) | 2004 | Gravedad | 10,5-16 | 72 | 2,3 | 6-9,5 | – | – | – |
| KENTISH FLATS (UK) | 2005 | Monopila | 5 | 30 | 3 | 3-5 | 4,88 | – | 0,9 |
| BARROW (UK) | 2006 | Monopila | 4,75 | 30 | 3 | 12-18 | 4,9 | – | 0,8 |
| THORNTON BANK (Bélgica) | 2006 | Gravedad | 6,5-17 | 60 | 5 | 10-24 | 6,32 | 11,06 | 1,2 |
| EGMOND AAN ZEE (Holanda) | 2007 | Monopila | 4,6 | 36 | 3 | 16-21 | 3,6 | 8 | 0,6 |
| LYNN AND INNER DOWSING (UK) | 2007 | Monopila | 4,74 | 54 | 3,6 | 6-13 | 2,38 | 7,03 | 0,9 |
| PRINCESS AMALIA (Q7) (Holanda) | 2008 | Monopila | 4 | 60 | 2 | 19-24 | 7,7 | 9,7 | 1,3 |
Durante la investigación se ha detectado la existencia de gran cantidad de información disponible sobre la producción energética, el emplazamiento o la geometría de diferentes parques eólicos offshore en Europa. Del mismo modo, y como se puede observar en la Tabla 1, se ha detectado también una gran carencia de información accesible sobre las variables climáticas tenidas en cuenta durante el diseño, como la altura de ola de diseño (HD) o el periodo pico (Tp). Esto se debe en gran medida a la confidencialidad presente en la documentación asociada a este tipo de proyectos.
En este sentido, y como aconseja la experiencia, sería útil poder disponer y conocer la relación existente entre la altura de ola y periodo en cada emplazamiento (T= f(H)). Relación que permitiría llevar a cabo el diseño de estas estructuras a través del conocimiento del clima marítimo. La caracterización de esta expresión no es objeto de este estudio, pero sí lo será dentro de futuras líneas de investigación del grupo.
Parámetro de altura de ola adimensional
El parámetro H0 se define como Hs/(Δ·D50), (siendo Hs la altura de ola significante, Δ, el coeficiente relativo de pesos específicos y D50, el diámetro característico de la grava, árido o arena) y se utiliza para clasificar diferentes estructuras. Ejemplo de ello son los cajones o estructuras similares de grandes dimensiones, que están relacionados con bajos valores de H0.
Van der Meer, en su Tesis Doctoral [4], consideró que en las costas rocosas o playas de grava donde el diámetro nominal medio de las mismas es relativamente pequeño, H0 se encuentra entre 6 y 20. De este modo, se podría afirmar que los parques eólicos con cimentaciones de tipo monopila o gravedad podrían pertenecer a este grupo, puesto que los diámetros de los elementos empleados en las protecciones dinámicas frente a la socavación presentan tamaños alrededor de 0,3 y 0,4 m
Para caracterizar H0 se emplearon los datos del clima marítimo (Hs, Tp) de los parques eólicos offshore seleccionados. Como se desarrollará más adelante en el epígrafe donde se recogen los resultados, se obtuvieron valores de H0 entre 6 y 15.
Diseño de las protecciones frente a la socavación
Actualmente, existen diferentes sistemas para llevar a cabo la protección frente a la socavación en parques eólicos marinos, como las protecciones basadas en escollera, los sistemas denominados “concrete pitching”, el empleo de bolsas de hormigón o sistemas denominados como “grouted fabric mattress” [5], o la colocación de un collar horizontal en el pié de la subestructura [6]. El sistema de protección más habitual hasta ahora se basa en el empleo de árido o escollera alrededor de cada uno de los aerogeneradores. Esto se debe al bajo coste de este material y a su sencilla disponibilidad, aunque esta técnica presenta en numerosas ocasiones problemas durante la instalación, ya que es susceptible a estar condicionada por las corrientes y/o el oleaje, de acuerdo a [5].
Con el fin de caracterizar estas protecciones, es importante definir el tamaño de la roca (D50), la extensión y el espesor de las capas de protección. Las protecciones frente al fenómeno de la socavación, en la mayoría de los casos están compuestas por dos diferentes capas, una capa inferior que actúa de filtro y una capa superior de armadura.
En la Tabla 2 se muestra el tamaño de la pieza (D50), y el espesor de las capas de filtro y protección (o manto) presentes en algunos de los parques eólicos marinos estudiados.
Tabla 2: Tamaño de la pieza (D50) y espesor de las capas de filtro y protección presentes en diferentes parques eólicos marinos.
| Nombre | D50 (m) | Espesor (m) |
|---|---|---|
| North Hoyle | 0,3 | Desconocido |
| Egmond aan Zee | 0,4 | 1,4 (manto) |
| Thornton Bank | 0,35 | 0,7 |
| Horn Rev | 0,2 (filtro); 0,4 (manto) | 0,5 (filtro); 1(manto) |
| Scroby Sands | 0,15 | Desconocido |
| Arklow Bank | 0,425 | Desconocido |
Como se puede observar, el tamaño de la pieza (D50) presente en las diferentes capas (filtro y protección) no es el mismo en cada caso, empleándose un menor tamaño en las capas de filtro.
La información disponible permitió confirmar que el espesor de la capa de protección empleado habitualmente es al menos dos veces el tamaño medio de árido D50 (ver Tabla 2), como recomienda [6], aunque encontrar información sobre dicha característica en el diseño de estas protecciones resultó ser complicado.
La Tabla 3 muestra las recomendaciones para el cálculo de la extensión de las protecciones de escollera propuestas por diferentes autores en los últimos años. Cabe destacar que dichas formulaciones fueron propuestas únicamente bajo condiciones de corriente continua.
Tabla 3: Recomendaciones para el cálculo de la extensión de las protecciones frente a la socavación de escollera.
| Autor | Extensión de las protección (Lext [m]) |
|---|---|
| Bonasoundas (1973) [7] | 2,5D-4,5D |
| Hjorth (1975) [8] | 2,5D |
| Breusers and Raudkivi (1991) [9] | 3D-4D |
| Hoffmans and Verheij (1997) [6] | 2,5D-4D |
| Melville and Coleman (2000) [10] | 3D-4D |
| May (2002) [11] | 2D |
Como se puede observar, los valores recogidos en la Tabla 3 sobre la máxima extensión de dicha protección se encuentran en función del diámetro de la pila (D). Omitiéndose de este modo variables climáticas como la altura de ola y el periodo, que juegan un papel importante en el diseño de estas estructuras.
Otros autores como [12] y [13], han desarrollado métodos para el cálculo de la extensión óptima de las protecciones frente a la socavación teniendo en cuenta la máxima profundidad de socavación (Smax), el ángulo de rozamiento interno en el fondo marino (Ø) y un factor de seguridad (Fs), definiendo la extensión de estas protecciones como:
(1) 
La conocida recomendación [14], para el diseño de parques eólicos offshore, propone la siguiente fórmula (2) para la estimación de la extensión de dichas protecciones frente a la socavación.
(2) 
Durante el estudio se analizaron formulaciones cuyas variables a tener en cuenta son la altura de ola y el periodo de oleaje. Esto hizo posible estudiar la interacción flujo estructura a través de dichos parámetros.
Un ejemplo de ello es el estudio de [15], donde se recoge que la extensión de la distribución de presiones en la berma (Lpb) calculada a través de la teoría de Sainflou es:
(3) 
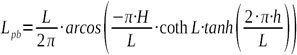
Considerando esta fórmula como una aproximación conservativa, podría ser razonable diseñar las protecciones frente a la socavación con dimensiones superiores a Lpb.
La Tabla 4 muestra la extensión de las protecciones frente a la socavación recomendadas por diferentes autores y calculadas en los parques eólicos marinos con suficiente información disponible. Como se observa, los valores calculados por la fórmula (3) oscilaron entre L/4 y L/2.
Los resultados obtenidos teniendo en cuenta la mayor extensión recomendada (4D) por diferentes autores ([6], [7], [9] o [10]) fueron mucho más conservadores que los propuestos por las recomendaciones de [14].
Tabla 4: Extensión de las protecciones frente a la socavación recomendadas por diferentes autores en los parques eólicos Europeos estudiados (Desarrollo propio).
| Nombre | Diámetro Monopila (m) | Lext (m) | |||||
|---|---|---|---|---|---|---|---|
| 4D | Cartens (1) | DNV (2) | Löffler (3) | L/4 | L/2 | ||
| N7 | 6 | 24 | 30,62 | 15,83 | 40 | 32,75 | 65,5 |
| SCARWEATHER SANDS | 2,2 | 8,8 | 13,64 | 6,82 | 14,22 | 12,1 | 24,21 |
| NORTH HOYLE | 4 | 16 | 24,26 | 12,16 | 17,06 | 13,88 | 27,76 |
| LYNN AND INNER | 4,74 | 18,96 | 28,34 | 16,33 | 14,25 | 14,77 | 29,55 |
| EGMOND AAN ZEE | 4,6 | 18,4 | 28,5 | 14,24 | 23,82 | 21,75 | 43,5 |
| PRINCESS AMALIA (Q7) | 4 | 16 | 24,8 | 13,4 | 34,61 | 29,82 | 59,64 |
En la Tabla 5 se muestran los valores de H0 calculados en cada uno de los parques eólicos marinos donde se dispuso de toda la información sobre el clima marítimo (Hs, Tp) y la protección frente a la socavación (D50) empleada. Siendo 
, γw=1.025 kg/m3 y γr=2.650 kg/m3.
Tabla 5: Valores de H0 de los parques eólicos europeos estudiados.
| Nombre | Diámetro Monopila [m] | Hs [m] | D50 [m] |  [m] |
|---|---|---|---|---|
| HORNS REV | 4,25 | 5,2 | 0,4 | 8,2 |
| NORTH HOYLE | 4 | 4,78 | 0,3 | 10,05 |
| SCROBY SANDS | 4,2 | 2,25 | 0,15 | 9,46 |
| ARKLOW BANK | 5 | 5,6 | 0,42 | 8,31 |
| THORNTON BANK | 6,5-17(GBS) | 6,32 | 0,35 | 11,39 |
| EGMOND AAN ZEE | 4,6 | 3,6 | 0,4 | 5,68 |
Como se puede observar en la Tabla 5, todos los valores de H0 salvo el correspondiente al parque Egmond Aan Zee toman valores entre 6 y 20, rango propuesto inicialmente. El valor próximo a 6 de Egmond Aan Zee se debe a la correlación existente entre H-T. En este parque eólico, el valor del periodo pico es reducido debido al viento, tema que debería ser estudiado y tenido en cuenta en el diseño de futuros parques eólicos.
Conclusiones
El diseño de protecciones frente a la socavación debería estar completamente integrado en el diseño de las cimentaciones desde el principio. Con el fin de llevar a cabo un diseño efectivo, las propiedades de los sedimentos, las características geotécnicas del fondo marino, los parámetros climáticos (Hs, Tp, etc.), las especificaciones de los aerogeneradores (diámetro, forma, etc.) deben tenerse en cuenta a la hora de predecir con precisión la máxima profundidad de socavación que podría producirse en ausencia de protección.
Sobre los datos empleados, se encontraron dificultades en la recopilación de información relacionada con las variables del clima marítimo y su correlación entre la altura de ola significante (Hs), el periodo pico (Tp) o el periodo medio (Tm), o la altura de momento centrado de orden cero (Hm0) y el periodo (T02).
Teniendo en cuenta esta investigación como un primer ajuste en el diseño de las protecciones frente a la socavación, sería aconsejable dimensionar estas estructuras con extensiones entre L/4 y L/2, mediante un material granular con dimensiones de (H0) entre 6 y 20.
Referencias
[1] Esteban, M.D.; Diez, J.J.; López, J.S., and Negro, V., 2009. “Integral Management applied to Offshore Wind Farms”, Journal of Coastal Research, SI 56, 1204-1208.
[2] Esteban, M.D.; Diez, J.J.; López, J.S., and Negro, V., 2011. “Methodology for the design of offshore wind farms”, Journal of Coastal Research, SI 64, 496-500.
[3] Wind Europe, “Offshore Wind in Europe. Key trends and statistics 2017”, Technical Report of European Wind Energy Association, 2012. https://windeurope.org/wp-content/uploads/files/about-wind/statistics/WindEurope-Annual-Offshore-Statistics-2017.pdf
[4] Van der Meer, J.W., 1988. “Rock slopes and gravel beaches under wave attack”, The Netherlands: TU Delft. Ph.D. Thesis, 214p.
[5] Rail Corp., 2007. “Scour Protections (S40)”, RailCorp Technical Specifications.
[6] Hoffmans, G.J.C.M. and Verheij, H.J., 1997. “Scour Manual”, Rotterdam, The Netherlands: A.A.Balkema, 205 p.
[7] Bonasoundas, M., 1973. “Strömungsvorgang und Kolkproblem am pfeiler, Versuchsanstalt für Wasserbau”, Bericht 28, Germany: Technischen Universität München, Oskar v. Miller Institut.
[8] Hjorth, P., 1975. “Studies on the nature of local scour”, Sweden, Institute of Technology, Dept. of Water Resources Engineering. Lund Institute of Technology, University of Lund, Bulletin, ser. A, no. 46, 191 p.
[9] Breusers, H.N.C. and Raudkivi, A.J., 1991. “Scouring”, Rotterdam, The Netherlands, Balkema, 143p.
[10] Melville, B.W. and Coleman, S.E., 2000. “Bridge scour”, USA: Water Resources Publications Highlands, 550p.
[11] May, R.W.P.; Ackers, J.C. and Kirby, A.M., 2002. “Manual on scour at bridges and other hydraulic structures”, CIRIA.
[12] Den Boon, J.H.; Sutherland, J.; Whitehouse, R.; Soulsby, R.; Stam, C.J.M.; Verhoeven, K.; Høgedal, M. and Hald, T., 2004. “Socur behavior and scour protection for monopile foundations of Offshore Wind Turbines”, EWEC (London, UK).
[13] Carstens, T., 1976. “Seabed scour by currents near platforms”, 3th Conference on port and ocean engineering under arctic conditions (University of Alaska), pp. 991-1006.
[14] Det Norske Veritas, 2011. “Design of Offshore Wind Turbine Structures”, Offshore Standard DNV-OS-J101.
[15] Löffler, A. and Kortenhaus, A., 1999. “Non breaking waves – Pressures on berms –“, Chapter 4.6. Mast III/PROVERBS. MAS· – CT95-0041. Final Report. Volume IIa. Hydrodynamic Aspects. Edited by N.W.H. Allsop.
